The Programming of a Chess Engine ♟️

About 2 weeks ago, I set out to build my own chess computer. The idea of writing a program that could beat me at something I do quite regularly was very intriguing. And it turned out to be one of the best programming experiences of my life. I found so much elegance, and the overall experience of building and iterating on it was very satisfying.
Representing Chess Positions – Bitboards
The very first thing we have to do is to think about how we're gonna represent a chess position, programmatically. But there's a much more efficient method we can use. The Bitboard method. Bitboards capitalize on the fact that a chessboard has 64 squares and a 64-bit integer also contains 64 bits of information. So we can represent the position of, say, all white pawns with one large number, where each bit corresponds to a specific square on the board.

If we now want to check if some square is occupied by any of these pawns, we can simply take that square bitboard, perform a bitwise AND operation with the pawns, and check for a non-zero result. It's things like this that enable the generation of possible moves. And when you're searching millions of positions a second, a significant amount of time is spent here. What we did now amounts to a handful of CPU instructions, so it's really fast.
Finally, the whole board could be represented by twelve of these bitboards, one for each piece type. Along with a few game rules, before we can go find the best move, we have to somehow be able to tell if a position is better than the other. We need an evaluation function, one that takes a chessboard as input, and outputs who's doing better.
Evaluation Function
Some positions are straightforward, like when someone has checkmated the other, or when it's a draw. So let's start here, we're going to assign a large, arbitrary number when white has won, and the negative of it when black has won. A draw will be a zero.
Now, when the game is yet to be decided, it's trickier, but generally capturing pieces indicates a strong position. So for starters, we assign values to each piece. A pawn will be a 1, and all the other pieces will be scored relative to it. By adding up the white pieces and subtracting the black ones, we get a score. The more positive the score, the better for white; the more negative, the better for black.
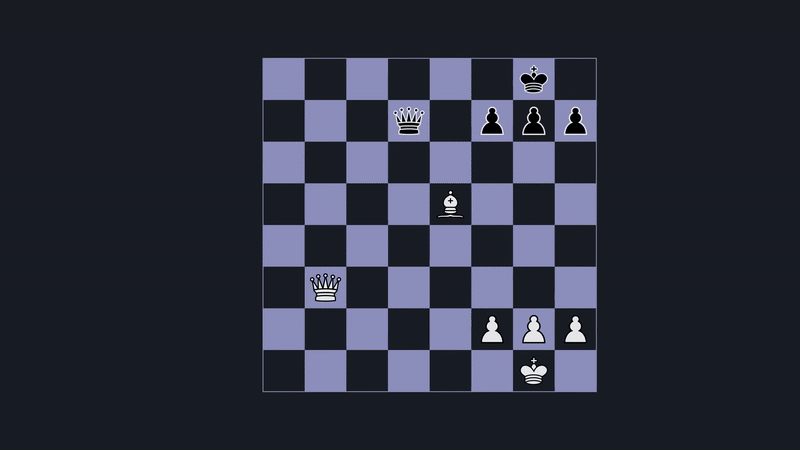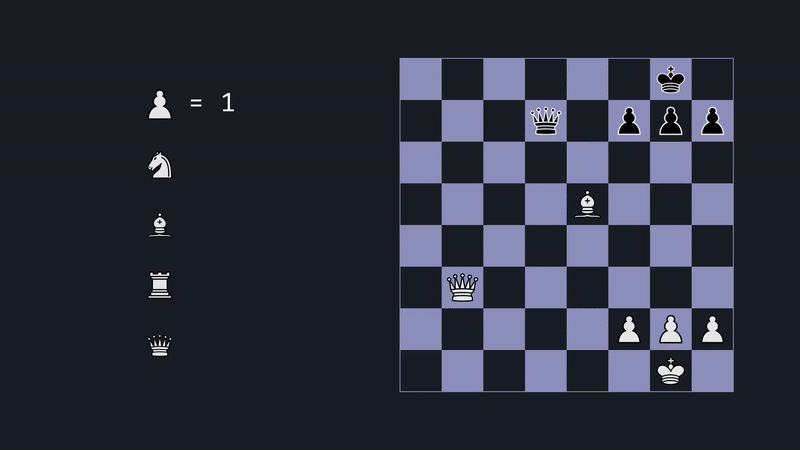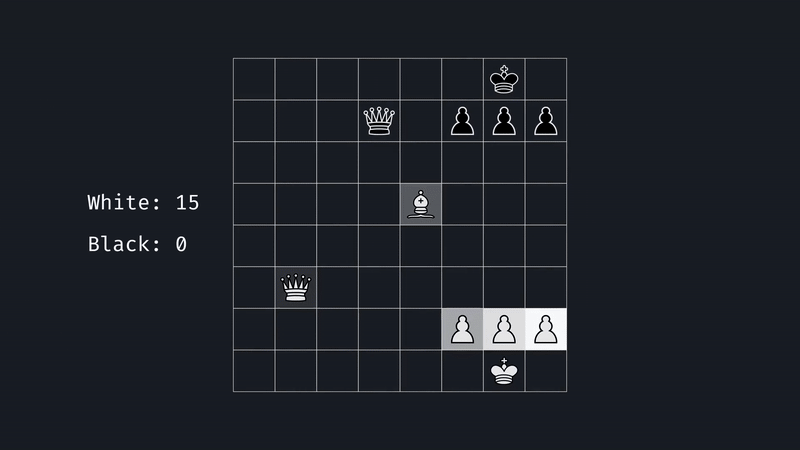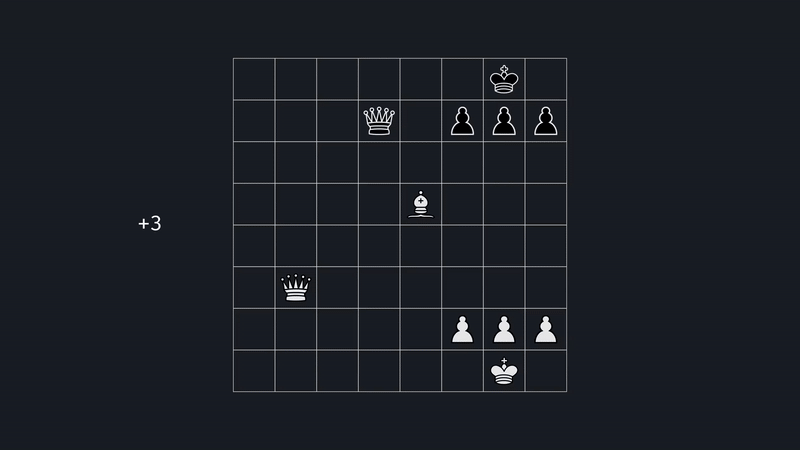
But let's not stop here; we can give our evaluation function a little more nuance by considering where a piece is located. See, a Knight in the middle is better than one on the edge, as it controls more squares. So for each square, we can adjust the piece's value by some amount. So now, when we count material, this Knight will be worth 3.25, and this one 2.5. We can do this for all piece types; for instance, the king generally wants to be tucked away in the corner. These adjustment values make a tremendous difference. It makes the engine make natural moves, placing pieces on active squares and prioritizing king safety.
Even though this way of defining a position's value is hardcoded, it is very sufficient for creating extremely strong chess engines, and the reason for that? search.
Searching the Game Tree
We start by extracting all the legal moves. We then make those moves and use the evaluation function to get a score. We do this for all the moves, and it seems like taking the pawn is the best move. However, if we calculate further, the black king will capture the rook, resulting in a draw. So taking the pawn is, of course, bad, and you should move your rook.
Had we taken black's response into consideration for every move, moving the rook would have maximised the eval. And this is what it's all about, searching down the game tree.
Minimax Algorithm
But now, let's do it properly, with the famous minimax algorithm. As input, it will take in a board and a depth, indicating how deep we will search, and it will return the best achievable evaluation.
To demonstrate, we will search to a depth of 2, meaning white makes a move and black responds. Or in other terms, we will consider white moves, and then black responses to those moves. Nodes will be orange when it's blacks turn to move. So let's call minimax on the starting position and initialize a variable with a low, arbitrary value. We will generate the moves, and then for each move, we will make that move, resulting in a new position. We then call minimax on that board, with depth-1.
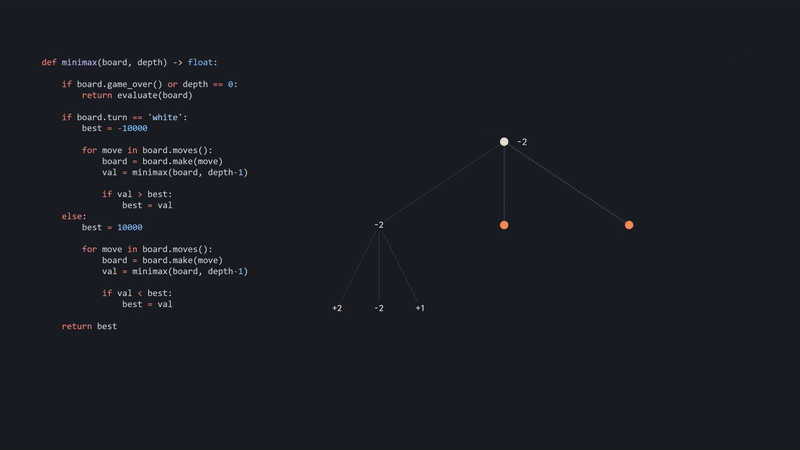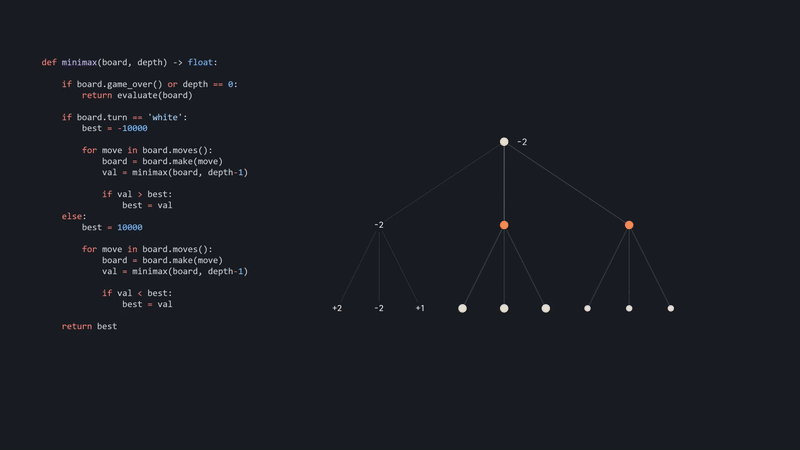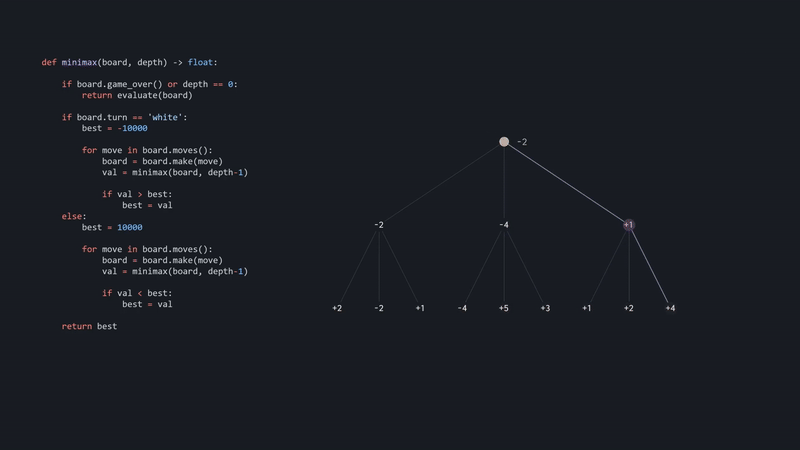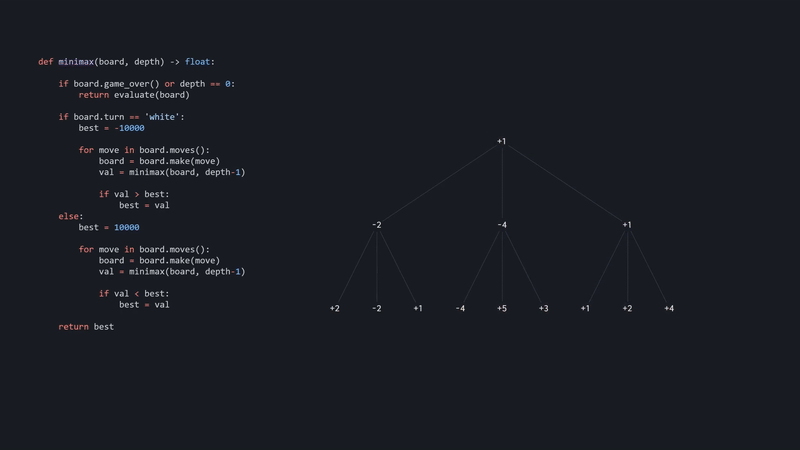
Now we are on a node where it's blacks turn, and black is trying to minimize the evaluation. So while we initialized it low for white, let's do it high for black. And then we do the same procedure as with white, iterating over all the moves. As with all recursion, we eventually have to return something, so let's call our evaluation function and return the result. Also, the game could be over before we reach our desired depth, so let's check for this too.
Since the returned value is lower than what we have found so far, we will assign it as the new best. We do this for all the moves, and eventually, when we're done, we're going to return that evaluation, taking us back to the starting position. Just like with black, let's save the result, compare it, and do this procedure for the remaining moves.
Alpha-Beta Pruning
If we take a closer look and rewind a little bit, just when white evaluated the first branch, then went down this path and found a -4, we know for sure that this node will be -4 or lower, since it's black choosing the moves. But since white has already found -2, it will never go down this branch, and so there is no need to evaluate the remaining positions. We can prune the search tree.
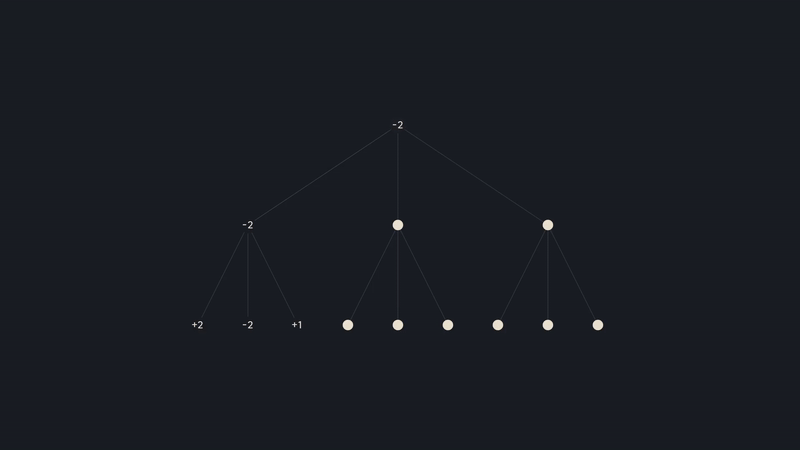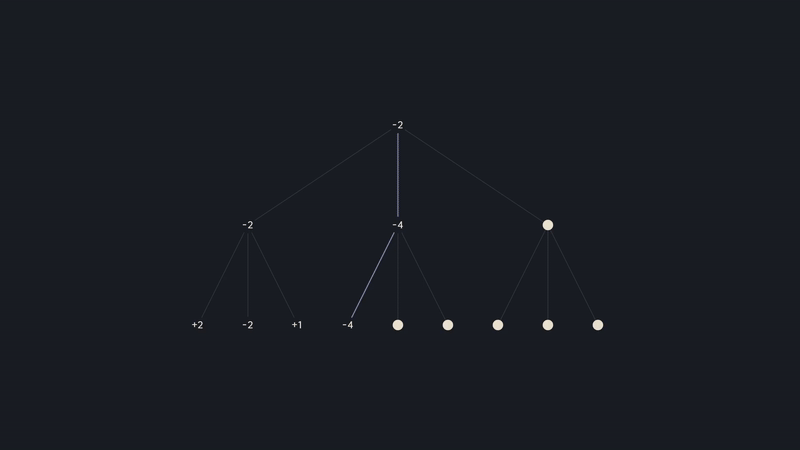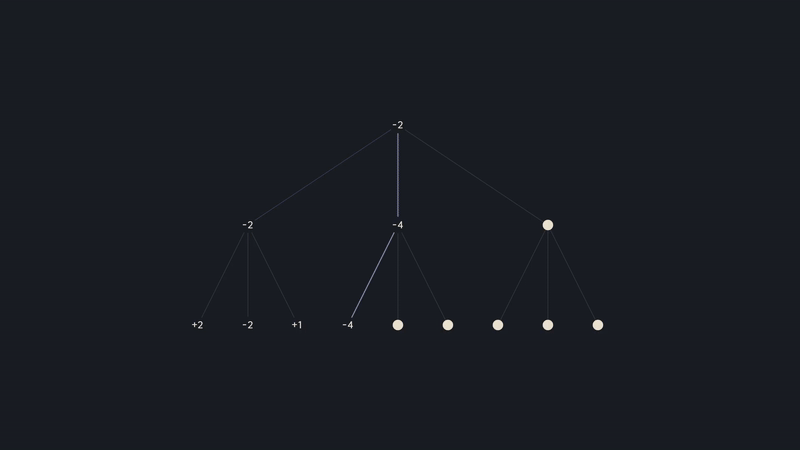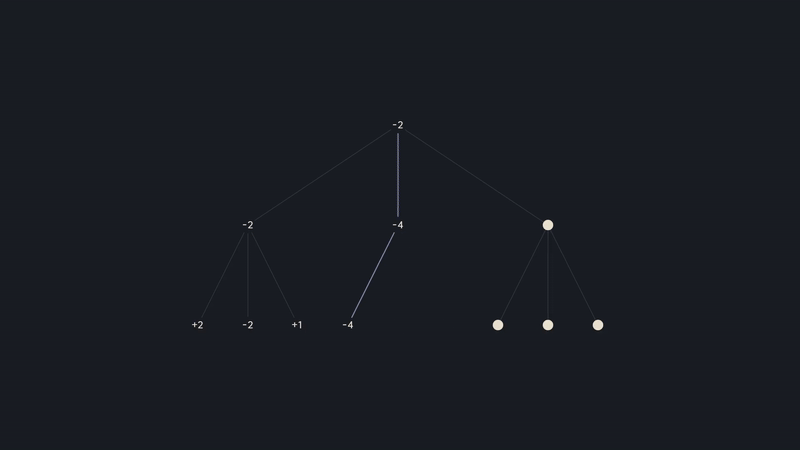
We would do this by implementing the alpha-beta algorithm, where you keep track of the best eval each side can force. I won't delve into the details here, since there is already a great video on it by Sebastian Lounge. You can check that out here!
End Note
There are many more optimizations you could make, but this was the very core of a chess engine. If you ever do decide to embark on this journey, there is a whole Wikipedia page about all of this. I wish you a happy day. Ciao!